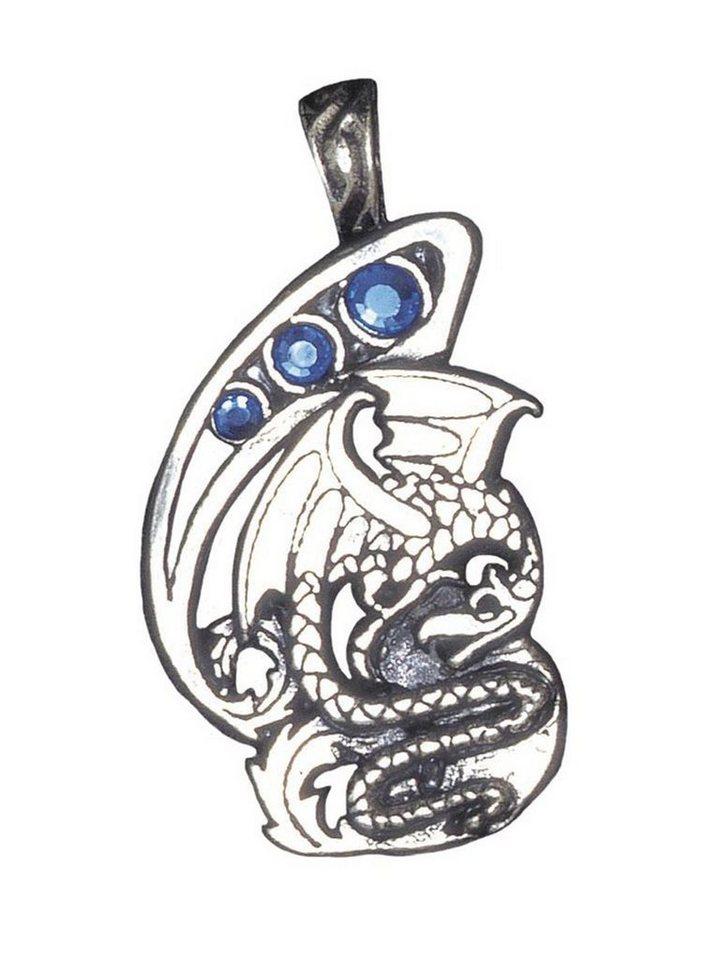
Adelia´s Amulett Anhänger Fire & Ice Talisman, Dra...
38,73 €
OTTO
ab 2,95 Versandkosten

Adelia´s Amulett Anhänger Fairy Magick Talisman, M...
38,73 €
OTTO
ab 2,95 Versandkosten

Adelia´s Amulett Anhänger Rob Ray Talisman, Kreuzf...
35,83 €
OTTO
ab 2,95 Versandkosten

Adelia´s Amulett Anhänger Das Erbe der Nordländer...
24,28 €
OTTO
ab 2,95 Versandkosten

Adelia´s Amulett Anhänger Rob Ray Talisman, Triski...
26,21 €
OTTO
ab 2,95 Versandkosten

Adelia´s Amulett Anhänger Fairy Magick Talisman, M...
38,83 €
OTTO
ab 2,95 Versandkosten

Sinus Art Leinwandbild 2 Bilder je 60x90cm Buch Ti...
37,00 €
OTTO
ab 7,00 Versandkosten

Pixi Wissen: Die Wikinger,1 Audio-CD - Monica Witt...
4,99 €
weltbild
ab 6,95 Versandkosten

Pixi Wissen: Tierrekorde,1 Audio-CD - Cordula Thör...
4,99 €
weltbild
ab 6,95 Versandkosten

Wissen für Vorschulkids. Was weißt du über die Erd...
19,95 €
weltbild
ab 0 Versandkosten

Geschlecht und Wissen(schaft) in Ostmitteleuropa,...
34,00 €
weltbild
ab 0 Versandkosten

STARK Abitur-Wissen Ethik - Freiheit und Determina...
17,95 €
weltbild
ab 0 Versandkosten

Rätsel X Wissen , Das Geheimnis des verlorenen Sch...
6,00 €
weltbild
ab 0 Versandkosten

Pixi Wissen 42: VE 5 Tiere der Welt - Jürgen Beckh...
9,95 €
weltbild
ab 0 Versandkosten

Wer hätte das gedacht?! Das Unnützes Wissen-Quiz K...
8,99 €
weltbild
ab 6,95 Versandkosten

Arbeitsmappe zu Leselauscher Wissen: Ritter und Bu...
7,90 €
weltbild
ab 0 Versandkosten

Physik - Ausgabe Volk und Wissen - Orientierungsst...
7,50 €
weltbild
ab 0 Versandkosten

Verbotenes Wissen - Jason Quitt, Bob Mitchell, Geb...
22,99 €
weltbild
ab 0 Versandkosten

Leselauscher Wissen: Roboter - Liliane Mika, Gebun...
15,00 €
weltbild
ab 0 Versandkosten

Das ultimative Wissens-Quiz - Philip Kiefer, Karto...
6,99 €
weltbild
ab 0 Versandkosten